Problem 2.6

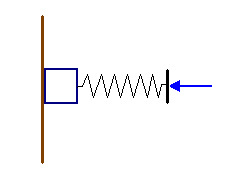
Un bloque de 500 g de masa permanece en equilibrio al ser presionado contra una pared mediante un resorte de constante de elasticidad 10 N/cm, como se indica en la figura. Si el coeficiente de fricción estática entre el bloque y la pared es 0,25, la mínima distancia, en cm, que se debe comprimir el resorte para que el bloque permanezca en equilibrio es: (g = 9,81 m/s²)

A) 0,49       B) 0,98       C) 1,96       D) 2,94       E) 3,23
SOLUCION

Problem 2.5

Un objeto pequeño, partiendo del reposo, cae desde una altura de 1 m sobre la superficie de la Luna. Calcule la velocidad final en m s^-1 con la cual el objeto llega a la superficie de la Luna. Se sabe que la masa de la Luna es 0,01255 veces la masa de la Tierra y el radio promedio de la Luna es 0,27300 veces el radio promedio de la Tierra. La aceleración de la gravedad terrestre es 9,81 ms^-2.

A) 0,98       B) 1,65       C) 1,82       D) 1,96       E) 2,12
SOLUCION

Problem 2.4

Considere la fuerza F(x) = F(x) i. La dependencia de F(x) con x se muestra en el gráfico. Calcule el trabajo realizado por la fuerza F (en J) al actuar sobre una partícula entre los puntos x = 0 y x = 15 m.

A) 182,5       B) 187,5       C) 287,5       D) 345,0       E) 402,5
SOLUCION

Problem 2.3

Sobre el platillo de una balanza se dejan caer, desde una altura de 2,74 m, partículas que chocan elásticamente con el platillo antes de perderse. Si cada partícula tiene una masa de 0,114 kg y caen 32 partículas por segundo, calcule la lectura de la balanza en N. (g = 9,81 m/s²)

A) 43,4       B) 53,4       C) 63,4       D) 73,4       E) 83,4
SOLUCION

Problem 2.2

La energía cinética de una partícula de 0,25 Kg de masa que realiza un MAS, atada a un resorte es: E_k = 0,2 - 20x², donde E_k está dada en Joules y x, la posición, en metros. Dadas las siguientes proposiciones:

I.     La energía mecánica del oscilador es 0,2 J.
II.   La amplitud de oscilación es 0,2 m.
III. La frecuencia angular de oscilación es 12,65 rad/s.

Indique la secuencia correcta después de determinar si la proposición es verdadera (V) o falsa (F).

A) VVV       B) VFF       C) VVF       D) VFV       E) FVV
SOLUCION

Problem 2.1

La figura muestra una onda que se propaga hacia la derecha a lo largo de una cuerda.

La frecuencia de la onda es f = 4 Hz. Dadas las siguientes proposiciones:

I.     El periodo de la onda es de o,25 s.
II.   La longitud de onda vale 20 cm.
III. La velocidad de propagación de la onda es de 1,6 m/s

¿Cuál de las siguientes alternativas presenta la secuencia correcta después de determinar si la proposición es verdadera (V) o falsa (F)?

A) VFF       B) VFV       C) FFV       D) VVF       E) FVF
SOLUCION

Problem 2.0

Un bloque cuya densidad es ρ, flota con las 3/4 partes de su volumen sumergido en un líquido. Entonces la densidad del líquido es:

A) ρ/4       B) ρ/3       C) 2ρ/3       D) 4ρ/3       E) 5ρ/3
SOLUCION

Problem 1.9

Un alambre tiene un coeficiente térmico de dilatación lineal de 2,5 x 10^-4 ºC^-1. ¿En cuántos grados Celsius debe elevar su temperatura para que su longitud se incremente en 2,5 %?

A) 40       B) 60       C) 80       D) 100       E) 120
SOLUCION

Problem 1.8

Un calentador tiene una resistencia de 100 Ω y está conectado a una tensión de 220 voltios. Considere que la capacidad calorífica del calentador es despreciable y que contiene un litro de agua a 20 ºC. Calcule el tiempo que se requiere para que el agua comience a hervir. Considere 1J = 0,24 cal.
SOLUCION

Problem 1.7

Suponga que un globo de forma esférica tiene sobre su superficie una distribución uniforme de carga negativa. El globo es inflado de manera que el área de su superficie varía desde A_i hasta A_f. Haga un gráfico que represente la correspondiente variación del potencial eléctrico V sobre la superficie del globo.
SOLUCION

Problem 1.6

El sistema de calentamiento de una ducha eléctrica está representado en la figura. Con la llave en la posición "invierno" la ducha disipa 2,200 W mientras que en la posición "verano" disipa 1,100 W. La tensión en la red de alimentación es de 110 V. Si asumimos que los valores de las resistencias no cambian con la temperatura, entonces la suma de los valores de R₁ y R₂ (en ohmios) es:

SOLUCION

Problem 1.5

Si disminuimos el periodo de rotación de la Tierra hasta alcanzar el valor T, observamos que al pesar un cuerpo de masa m en el Ecuador, la balanza marca cero. Si el radio de la Tierra en el Ecuador es R = 6,4 x 10⁶ m, su período de rotación es T_o = 3π x 10⁴ s y la aceleración de la gravedad en la superficie de la Tierra es g = 9,81 m/s² , calcule T/T_o.
SOLUCION

Problem 1.4

Un objeto de 3,0 cm de altura se sitúa a 20,0 cm de un espejo convexo que tiene una distancia focal de 8,0 cm. Calcule en cm la altura de la imagen.
SOLUCION

Problem 1.3

Se ilumina una superficie metálica con luz de 780 nm de longitud de onda detectándose que se emiten electrones con una energía cinética máxima de 0,37eV. ¿Cuál sería la energía cinética máxima de los electrones en eV si se ilumina la superficie con luz de 410 nm? (constante de Planck = 4,14 x 10^-15 eV.s; velocidad de la luz = 3 x 10⁸ m/s)
SOLUCION

Problem 1.2

[ NOTACIÓN: "sqrt(m)" léase "raíz cuadrada de m" ]

A través de la espira rectangular de la figura pasa un campo magnético de 2 T, paralelo al eje X. Si el campo disminuye uniformemente hasta anularse en un intervalo de sqrt(3) segundos. ¿Cuál es la fuerza electromotriz (en V) inducida en la espira?

SOLUCION

Problem 1.1

[ NOTACIÓN: "m (AM" léase "Medida del Arco AM" ]

En la figura, ABC es un triángulo, su circunradio mide R = 6 m y su inradio r = 2 m. Calcule x + y + z en metros, si m (AM = m (MB ; m (BN = m (NC y m (AQ = m (QC.

SOLUCION